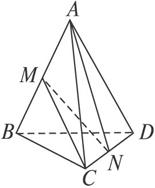
(1)求证:MN为AB和CD的公垂线;
(2)求MN的长;
(3)求异面直线AN与MC所成角的余弦值.
(1)求证:MN为AB和CD的公垂线;
(2)求MN的长;
(3)求异面直线AN与MC所成角的余弦值.
=p,
=q，
=r，(1)证明：
=
（
）-
=
(q+r-p
所以
·
=
（q+r-p
(q·p+r·p-p2)=
(a2·cos60°+a2·cos60°-a2)=0.所以MN⊥AB，同理可证MN⊥CD.
所以MN为AB与CD的公垂线.
(2)解
:由(1)可知
=
(q+r-p),所以|
|2=(
)2=
(q+r-p
［q2+r2+p2+2(q·r-q·p-r·p)］=
［a2+a2+a2+2(
-
-
)］=
×2a2=
.所以|
|=
a.
所以MN的长度为
a.
(3)解
:设向量
与
的夹角为θ,因为
=
(
)=
(q+r
=
-
=q
p,所以
·
=
(q+r
p)=
(q
q·p+r·q-
r·p)=
(a2-
a2·cos60°+a2cos60°-
a2·cos60°)
=
(a2-
+
-
)=
.
又因为|
|=|
|=
a,
所以
·
=|
|·|
|·cosθ
=
a·
a·cosθ=
.
所以cosθ=
.
所以向量
与
的夹角余弦值为
.
从而异面直线AN,MC所成角的余弦值为
.