已知定义域为R的二次函数f（x）的最小值为0且有f（1+x）=f（1－x），直线g（x）=4（x－1）被f（x）的图像截得的弦长为
，数列{an}满足a1=2，
（Ⅰ）求函数f（x）
（Ⅱ）求数列{an}的通项公式
（Ⅲ）设
已知定义域为R的二次函数f（x）的最小值为0且有f（1+x）=f（1－x），直线g（x）=4（x－1）被f（x）的图像截得的弦长为，数列{an}满足a1=2，
（Ⅰ）求函数f（x）
（Ⅱ）求数列{an}的通项公式
（Ⅲ）设
解：（Ⅰ）设
，则直线g（x）=4（x－1）与y=f（x）图象的两个交点为（1，0）（
（Ⅱ）
数列{an－1}是首项为1，公比为
的等比数列 
（Ⅲ）
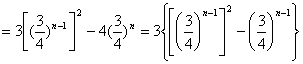
则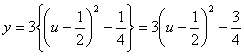
∵n∈N*，u的值分别为1，
；经比较
最近
∴当n=3时，bn有最小值是
当n=1时，bn有最大值是0