已知函数
有且只有一个零点，其中
．
（Ⅰ）求
的值；
（Ⅱ）若对任意的
，有
成立，求实数
的最大值；
（Ⅲ）设
，对任意
, 证明：不等式
恒成立．
已知函数有且只有一个零点，其中．
（Ⅰ）求的值；
（Ⅱ）若对任意的，有成立，求实数的最大值；
（Ⅲ）设，对任意, 证明：不等式恒成立．
解：（Ⅰ）f（x）的定义域为（﹣a，+∞），
．
由f'（x）=0，得x=1﹣a＞﹣a．
∵当﹣a＜x＜1﹣a时，f'（x）＞0；当x＞1﹣a时，f'（x）＜0，
∴f（x）在区间（﹣a，1﹣a]上是增函数，在区间[1﹣a，+∞）上是减函数，
∴f（x）在x=1﹣a处取得最大值．
由题意知f（1﹣a）=﹣1+a=0，解得a=1．
（Ⅱ）由（Ⅰ）知f（x）=ln（x+1）﹣x，
当k≥0时，取x=1得，f（1）=ln2﹣1＜0，知k≥0不合题意．
当k＜0时，设g（x）=f（x）﹣kx2=ln（x+1）﹣x﹣kx2．
则
令g/（x）=0，得x1=0，
．
①若
≤0，即k≤﹣
时，g'（x）＞0在x∈（0，+∞）上恒成立，
∴g（x）在[0，+∞）上是增函数，从而总有g（x）≥g（0）=0，
即f（x）≥kx2在[0，+∞）上恒成立．
②若
，即
时，对于
，g'（x）＜0，
∴g（x）在
上单调递减．
于是，当取
时，g（x0）＜g（0）=0，即f（x0）≥
不成立．
故不合题意．
综上，k的最大值为
．
（Ⅲ） 由h（x）=f（x）+x=ln（x+1）．
不妨设x1＞x2＞﹣1，则要证明
，
只需证明
，
即证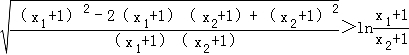
，
即证
．
设
，则只需证明
，
化简得
．
设
，则
，
∴φ（t）在（1，+∞）上单调递增，
∴φ（t）＞φ（1）=0．
即
，得证．
故原不等式恒成立．