(22分)如图所示,直角坐标系xoy位于竖直平面内,在 ‑ m≤ x ≤0的区域内有磁感应强度大小B = 4.0×10-4T、方向垂直于纸面向里的条形匀强磁场,其左边界与x轴交于P点;在x>0的区域内有电场强度大小E = 4N/C、方向沿y轴正方向的条形匀强电场,其宽度d =2m。一质量m = 6.4×10-27kg、电荷量q = -3.2×10-19C的带电粒子从P点以速度V = 4×104m/s,沿与x轴正方向成α=60°角射入磁场,经电场偏转最终通过x轴上的Q点(图中未标出),不计粒子重力。求:
m≤ x ≤0的区域内有磁感应强度大小B = 4.0×10-4T、方向垂直于纸面向里的条形匀强磁场,其左边界与x轴交于P点;在x>0的区域内有电场强度大小E = 4N/C、方向沿y轴正方向的条形匀强电场,其宽度d =2m。一质量m = 6.4×10-27kg、电荷量q = -3.2×10-19C的带电粒子从P点以速度V = 4×104m/s,沿与x轴正方向成α=60°角射入磁场,经电场偏转最终通过x轴上的Q点(图中未标出),不计粒子重力。求:
⑴带电粒子在磁场中运动时间;
⑵当电场左边界与y轴重合时Q点的横坐标;
⑶若只改变上述电场强度的大小,要求带电粒子仍能通过Q点,讨论此电场左边界的
横坐标x′与电场强度的大小E′的函数关系。

(22分)
解:(1)带电粒子在磁场中做匀速圆周运动
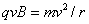 ------------------------(2分)
------------------------(2分)
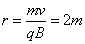 ------------------------(2分)
------------------------(2分)
由几何关系可知,粒子运动轨迹所对应的圆心角为600
且过Y轴时速度刚好平行于X轴
 ------------------------(2分)
------------------------(2分)
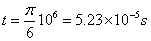 ------------------------(2分)
------------------------(2分)
(2)
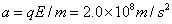 ------------------------(2分)
------------------------(2分)
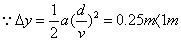
 粒子先做类平抛再做斜向匀速直线运动到Q点
粒子先做类平抛再做斜向匀速直线运动到Q点
设出场时速度方向与X轴夹角为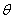
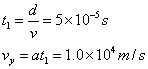
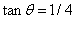 ------------------------(2分)
------------------------(2分)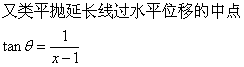 ------------------------(2分)
------------------------(2分)
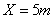 ------------------------(2分)
------------------------(2分)
(3)设电场左边界的横坐标为X/
讨论: i 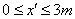
粒子先水平匀速后类平抛再斜向匀速到Q点
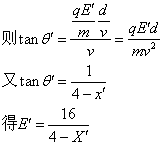 ------------------------(3分)
------------------------(3分)
ii 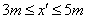
粒子先水平匀速再类平抛过Q点
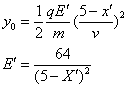 ------------------------(3分)
------------------------(3分)
![]() m≤ x ≤0的区域内有磁感应强度大小B = 4.0×10-4T、方向垂直于纸面向里的条形匀强磁场,其左边界与x轴交于P点;在x>0的区域内有电场强度大小E = 4N/C、方向沿y轴正方向的条形匀强电场,其宽度d =2m。一质量m = 6.4×10-27kg、电荷量q = -3.2×10-19C的带电粒子从P点以速度V = 4×104m/s,沿与x轴正方向成α=60°角射入磁场,经电场偏转最终通过x轴上的Q点(图中未标出),不计粒子重力。求:
m≤ x ≤0的区域内有磁感应强度大小B = 4.0×10-4T、方向垂直于纸面向里的条形匀强磁场,其左边界与x轴交于P点;在x>0的区域内有电场强度大小E = 4N/C、方向沿y轴正方向的条形匀强电场,其宽度d =2m。一质量m = 6.4×10-27kg、电荷量q = -3.2×10-19C的带电粒子从P点以速度V = 4×104m/s,沿与x轴正方向成α=60°角射入磁场,经电场偏转最终通过x轴上的Q点(图中未标出),不计粒子重力。求: 

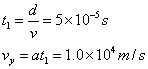
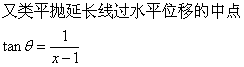
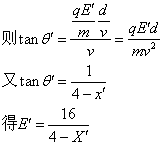
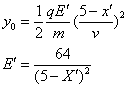 ------------------------(3
------------------------(3