(满分13分)如图12.1,已知抛物线经过坐标原点O和x轴上另一点E(4,0),顶点M的坐标为 (m,4),直角梯形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且BC=1,AD=2,AB=3.
(1)求m的值及该抛物线的函数关系式;
(2)将直角梯形ABCD以每秒1个单位长度的速度从图12.1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向点B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图12.2所示).
① 当t为何值时,△PNC是以PN为底边的等腰三角形 ;
② 设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
(1)由已知,根据抛物线的轴对称性,得m=2,
∴ 顶点M的坐标为(2,4), ………………(1分)
故可设其关系式为y=a(x-2)2+4.
又抛物线经过O(0,0),于是得a(0-2)2+4=0,解得 a=-1. ………(3分)
∴ 所求函数关系式为y=-(x-2)2+4,即y=-x2+4x. ………(4分)
(2)① ∵ 点A在x轴的正半轴上,且N在抛物线上,CB⊥PN,
∴ OA=AP=t,
∴ 点P,B,N的坐标分别为(t,t),(t,3),(t, -t2+4t).
∴ BP=3-t,AN= -t2+4t(0≤t≤3).
∴ PN=AN-AP=(-t2+4t)-t=-t2+3t=t(3-t)≥0. ………(6分)
要使得△PNC是以PN为底边的等腰三角形,
只需PN=2BP,即-t2+3t=2(3-t),
整理,得t2-5t+6=0,解得 t1=2,t2=3.
当t=3时,P,N两点重合,不符合题意,舍去.
∴ 当t=2时,△PNC是以PN为底边的等腰三角形. ………(8分)
② S存在最大值. ………(9分)
(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形.
若t=0,则S=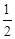 AD·AB=
AD·AB=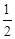 ·3·2=3.
·3·2=3.
若t=3,则S=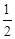 BC·AB=
BC·AB=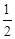 ·1·3=
·1·3=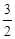 .
.
(ⅱ)当PN≠0,即0<t<3时,以点P,N,C,D为顶点的多边形是四边形.
 连结PD,CN,则
连结PD,CN,则
S=S四边形ANCD-S△ADP= S梯形ABCD+S△BCN -S△ADP
=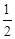 (BC+AD)·AB+
(BC+AD)·AB+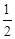 BN·BC-
BN·BC-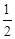 AP·AD
AP·AD
=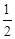 (1+2)·3+
(1+2)·3+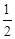 (-t2+4t- 3)·1-
(-t2+4t- 3)·1-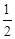 t·2
t·2
=-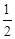 t2+t+ 3=-
t2+t+ 3=-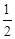 (t-1)2+
(t-1)2+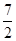 .
.
由-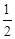 <0,0<t<3,当t=1时,S最大=
<0,0<t<3,当t=1时,S最大=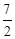 .
.
综上所述,当t=1时,以点P,N,C,D为顶点的多边形面积有最大值,
这个最大值为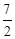 . ………………(13分)
. ………………(13分)
解析:略


 连结PD,CN,则
连结PD,CN,则 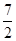 .
. 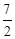 .
.