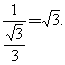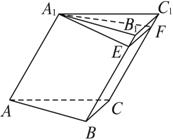
(1)求证：平面A1EF⊥平面B1BCC1；
(2)求直线AA1到平面B1BCC1的距离；
(3)当AA1多长时，点A1到平面ABC与平面B1BCC1的距离相等?
(1)求证：平面A1EF⊥平面B1BCC1；
(2)求直线AA1到平面B1BCC1的距离；
(3)当AA1多长时，点A1到平面ABC与平面B1BCC1的距离相等?
∴CC1⊥平面A1EF，∴平面A1EF⊥平面B1BCC1.
(2)作A1H⊥EF于H，则A1H⊥面B1BCC1，∴A1H为A1到面B1BCC1的距离.在△A1EF中，A1E＝A1F＝2，EF＝2，∴△A1EF为等腰直角三角形且EF为斜边，∴A1H为斜边上中线，可得A1H＝
EF＝1.
(3)作A1G⊥面ABC于G，连结AG，则A1G就是A1到面ABC的距离，且AG是∠BAC的角平分线，A1G＝1.
∵cos∠A1AG＝
.∴sin∠A1AG＝
.∴A1A＝