如图,在棱台![]() 中,
中,![]() 与
与![]() 分别是棱长为1与2的正三角形,平面
分别是棱长为1与2的正三角形,平面![]()
![]() 平面
平面![]()
![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形,![]() ,点
,点![]() 为
为![]() 的重心,
的重心,![]() 为
为![]() 中点,
中点,![]() ,
,
(1)当![]() 时,求证:
时,求证:![]() //平面
//平面![]() ;
;
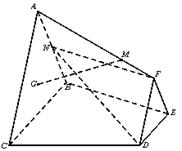 (2)若直线
(2)若直线![]() 与
与![]() 所成角为
所成角为![]() ,试求二面角
,试求二面角![]() 的余弦值.
的余弦值.
如图,在棱台![]() 中,
中,![]() 与
与![]() 分别是棱长为1与2的正三角形,平面
分别是棱长为1与2的正三角形,平面![]()
![]() 平面
平面![]()
![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形,![]() ,点
,点![]() 为
为![]() 的重心,
的重心,![]() 为
为![]() 中点,
中点,![]() ,
,
(1)当![]() 时,求证:
时,求证:![]() //平面
//平面![]() ;
;
 (2)若直线
(2)若直线![]() 与
与![]() 所成角为
所成角为![]() ,试求二面角
,试求二面角![]() 的余弦值.
的余弦值.
解:(Ⅰ)连![]() 延长交
延长交![]() 于
于![]() ,
,
因为点![]() 为
为![]() 的重心,所以
的重心,所以![]()
又![]() ,所以
,所以![]() ,所以
,所以![]() //
//![]() ;···················3(分)
;···················3(分)
![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点,
中点, ![]() //
//![]() ,又
,又![]() //
//![]() ,
,
所以![]() //
//![]() ,得
,得![]() 四点共面
四点共面
![]() //平面
//平面![]() ··································6(分)
··································6(分)
(Ⅱ)平面![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,连接
,连接![]() 易得
易得![]() ,
,
以![]() 为原点,
为原点,![]() 为x轴,
为x轴,![]() 为y轴,
为y轴,![]() 为z轴建立空间直角坐标系,
为z轴建立空间直角坐标系,
则![]() ,设
,设![]() ,
,
![]()
![]() ,
, ![]() ,
,![]()
因为![]() 与
与![]() 所成角为
所成角为![]() ,所以
,所以 ,
,
得![]() ,
,![]() ,
,![]() ,··············8(分)
,··············8(分)
设平面![]() 的法向量
的法向量![]() ,则
,则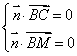 ,取
,取![]() ,
,
平面![]() 的法向量
的法向量![]() ,所以二面角
,所以二面角![]() 的余弦值
的余弦值 ····················12(分)
····················12(分)