(本小题满分14分)已知函数![]()
![]() .
.
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)判断函数![]() 在
在![]() 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ,求实数
,求实数![]() 与
与![]() 的值;
的值;
(本小题满分14分)已知函数![]()
![]() .
.
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)判断函数![]() 在
在![]() 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ,求实数
,求实数![]() 与
与![]() 的值;
的值;
(本小题满分14分)
解: (1)由![]() 得函数
得函数![]() 的定义域为
的定义域为![]() , ………………2分
, ………………2分
又![]()
所以![]() 为奇函数。 ……………………………………………………………4分
为奇函数。 ……………………………………………………………4分
(2)由(1)及题设知:![]() ,设
,设![]() ,
,
∴当![]() 时,
时,![]() ∴
∴![]() . ……6分
. ……6分
当![]() 时,
时,![]() ,即
,即![]() .
.
∴当![]() 时,
时,![]() 在
在![]() 上是减函数.
上是减函数.
同理当![]() 时,
时,![]() 在
在![]() 上是增函数. ………………………………8分
上是增函数. ………………………………8分
(3)①当![]() 时,有
时,有![]() .
.
由(2)可知:![]() 在
在![]() 为增函数,………………………………………9分
为增函数,………………………………………9分
由其值域为![]() 知
知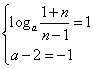 ,无解 …………………………………11分
,无解 …………………………………11分
②当![]() 时,有
时,有![]() .由(2)知:
.由(2)知:![]() 在
在![]() 为减函数,
为减函数,
由其值域为![]() 知
知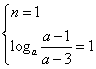 ……………………………………………13分
……………………………………………13分
得![]() ,
,![]() . ………………………………………………………14分
. ………………………………………………………14分