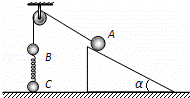
如图所示,A、B两小球由绕过轻质定滑轮的细线相连,A放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C球放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A的质量为4m,B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放A后,A沿斜面下滑至速度最大时C恰好离开地面.下列说法正确的是( )
| | A. | 斜面倾角α=30° |
| | B. | A获得最大速度为2g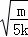 |
| | C. | C刚离开地面时,B的加速度最大 |
| | D. | 从释放A到C刚离开地面的过程中,A、B两小球组成的系统机械能守恒 |
考点:
机械能守恒定律;动能和势能的相互转化.版权所有 | | 专题: | 机械能守恒定律应用专题. |
| 分析: | C球刚离开地面时,弹簧的弹力等于C的重力,根据牛顿第二定律知B的加速度为零,B、C加速度相同,分别对B、A受力分析,列出平衡方程,求出斜面的倾角. A、B、C组成的系统机械能守恒,初始位置弹簧处于压缩状态,当B具有最大速度时,弹簧处于伸长状态,根据受力知,压缩量与伸长量相等.在整个过程中弹性势能变化为零,根据系统机械能守恒求出B的最大速度,A的最大速度与B相等; |
| 解答: | 解:A、C刚离开地面时,对C有:kx2=mg 此时B有最大速度,即aB=aC=0 则对B有:T﹣kx2﹣mg=0 对A有:4mgsinα﹣T=0 以上方程联立可解得:sinα=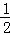 ,α=30°,故A正确; ,α=30°,故A正确; B、初始系统静止,且线上无拉力,对B有:kx1=mg 由上问知x1=x2=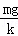 ,则从释放至C刚离开地面过程中,弹性势能变化量为零; ,则从释放至C刚离开地面过程中,弹性势能变化量为零; 此过程中A、B、C组成的系统机械能守恒,即: 4mg(x1+x2)sinα=mg(x1+x2)+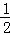 (4m+m)vBm2 (4m+m)vBm2 以上方程联立可解得:vBm=2g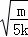 所以A获得最大速度为2g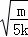 , , 故B正确; C、对B球进行受力分析可知,C刚离开地面时,B的速度最大,加速度为零.故C错误; D、从释放A到C刚离开地面的过程中,A、B、C及弹簧组成的系统机械能守恒,故D错误. 故选AB |
| 点评: | 本题关键是对三个小球进行受力分析,确定出它们的运动状态,再结合平衡条件和系统的机械能守恒进行分析. |

