已知在平面直角坐标系xoy中的一个椭圆，它的中心在原点，左焦点为
，右顶点为D（2，0），设点A的坐标是
（1）求该椭圆的标准方程；
（2）若P是椭圆上的动点，求线段PA中点M的轨迹方程；
（3）过原点O的直线交椭圆于点B、C，求△ABC面积的最大值.
已知在平面直角坐标系xoy中的一个椭圆，它的中心在原点，左焦点为，右顶点为D（2，0），设点A的坐标是
（1）求该椭圆的标准方程；
（2）若P是椭圆上的动点，求线段PA中点M的轨迹方程；
（3）过原点O的直线交椭圆于点B、C，求△ABC面积的最大值.
解：（1）设椭圆方程为
由题意得
=1
∴椭圆方程为
（2）设
由中点坐标公式
即为中点M的轨迹方程
（3）若直线BC斜率不存在，此时BC所在直线垂直x轴，
易得S△ABC=1
若直线BC斜率存在，设直线BC所在方程为y=kx，
并设B（x2，y2），C（x3，y3）
①当k=0时，S2=1.
②当k>0时，S2<1
③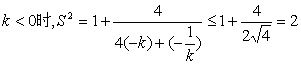
当且仅当
时，取“二”
综上所述△ABC面积的最大值为