18.设{an}为等差数列,{bn}为等比数列,a1=b1=1,a2+a4=b3,b2b4=a3.分
18.设{an}为等差数列,{bn}为等比数列,a1=b1=1,a2+a4=b3,b2b4=a3.分别求出{an}及{bn}的前10项的和S10及T10.
18.解:∵{an}为等差数列,{bn}为等比数列,∴a2+a4=2a3,b2b4=b32.
已知a2+a4=b3,b2b4=a3,∴b3=2a3,a3=b32.得b3=2b32.
∵b3≠0,∴b3=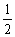
,
a3=
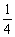
.
由a1=1,a3=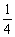
知{
an}的公差为
d=-
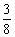
,
∴S10=10a1+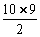
d=-
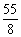
.
由b1=1,b3=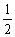
知{
bn}的公比为
q=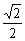
或
q=-
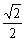
.
当q=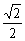
时,
T10=
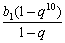
=
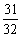
(2+
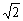
),
当q=-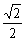
时,
T10=
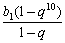
=
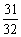
(2-
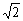
).
![]()
![]()
![]()
![]()
![]()
![]()
![]()