如图,折叠长方形一个角,点D落在BC边的点F处,BC=10㎝,AB=8㎝,求
如图,折叠长方形一个角,点D落在BC边的点F处,BC=10㎝,AB=8㎝,求:【小题1】求:FC的长度;
【小题2】求:EF的长度.

【小题1】(1)∵由题意得△AFE是由△ADE翻折得到的,
∴△AFE和△ADE关于直线AE对称,
∴AF=AD,EF=DE,
∵在长方形ABCD中,AD=BC=10,CD=AB=8,
∴AF=AD=10,
∵∠B=90
O,
∴在Rt△ABF中,BF
2=AF
2-AB
2=10
2-8
2=36,
∴BF=6,
∴FC=BC-BF=10-6=4(㎝).
【小题2】(2)设EF的长度为
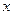
㎝,则DE=EF=
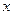
㎝,CE=CD-DE=(8-
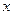
)㎝,
∵∠C=90
O,
∴在Rt△EFC中,FC
2+CE
2=EF
2,即4
2+(8-
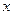
)
2=
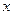 2
2;
解这个方程得:
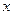
=5,
∴EF=5(㎝).解析:
p;【解析】略


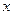 ㎝,则DE=EF=
㎝,则DE=EF=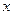 ㎝,CE=CD-DE=(8-
㎝,CE=CD-DE=(8-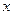 )㎝,
)㎝,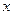 )2=
)2=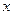 2;
2;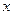 =5,
=5,