(理)已知函数f(x)=xlnx.
(1)求函数f(x)的单调区间和最小值;
(2)当b>0时,求证:bb≥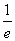 (其中e=2.718 28…是自然对数的底数);
(其中e=2.718 28…是自然对数的底数);
(3)若a>0,b>0,证明f(a)+(a+b)ln2≥f(a+b)-f(b).
(文)已知向量m
=(x
2,y-cx),
n=(1,x+b)(x,y,b,c∈R)且
m∥
n,把其中x,y所满足的关系式记为y=f(x).若f′(x)为f(x)的导函数,F(x)=f(x)+af′(x)(a>0),且F(x)是R上的奇函数.
(1)求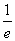 和c的值.
和c的值.
(2)求函数f(x)的单调递减区间(用字母a表示).
(3)当a=2时,设0<t<4且t≠2,曲线y=f(x)在点A(t,f(t))处的切线与曲线y=f(x)相交于点B(m,f(m))(A与B不重合),直线x=t与y=f(m)相交于点C,△ABC的面积为S,试用t表示△ABC的面积S(t),并求S(t)的最大值.
答案:
(理)解:(1)∵f′(x)=lnx+1(x>0),
令f′(x)≥0,即lnx≥-1=lne-1.∵e=2.718 28…>1,∴y=lnx在(0,+∞)上是单调递增函数.
∴x≥e-1=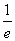 .∴x∈[
.∴x∈[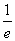 ,+∞).同理,令f′(x)≤0可得x∈(0,
,+∞).同理,令f′(x)≤0可得x∈(0,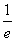 ].∴f(x)的单调递增区间为[
].∴f(x)的单调递增区间为[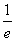 ,+∞),单调递减区间为(0,
,+∞),单调递减区间为(0,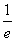 ].
].
由此可知y=f(x)min=f(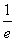 )=
)=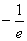 .
.
(2)证明:由(1)可知当b>0时,有f(b)≥f(x)min=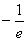 ,∴blnb≥
,∴blnb≥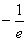 ,
,
即ln(bb)≥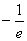 =ln(
=ln(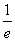 )
)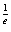 .∴bb≥(
.∴bb≥(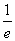 )
)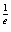 .
.
(3)证明:将f(a)+(a+b)ln2≥f(a+b)-f(b)变形,得f(a)+f(b)≥f(a+b)-(a+b)ln2,
即证f(a)+f(a+b-a)≥f(a+b)-(a+b)ln2.设函数g(x)=f(x)+f(k-x)(k>0).
∵f(x)=xlnx,∴g(x)=xlnx+(k-x)ln(k-x).∴0<x<k.∵g′(x)=lnx+1-ln(k-x)-1=ln ,
,
令g′(x)>0,则有 >1
>1
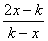 >0
>0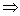
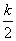 <x<k.
<x<k.
∴函数g(x)在[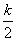 ,k)上单调递增,在(0,
,k)上单调递增,在(0,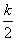 ]上单调递减.∴g(x)的最小值为g(
]上单调递减.∴g(x)的最小值为g(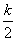 ),即总有g(x)≥g(
),即总有g(x)≥g( ).而g(
).而g( )=f(
)=f( )+f(k-
)+f(k-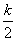 )=kln
)=kln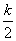 =k(lnk-ln2)=f(k)-kln2,∴g(x)≥f(k)-kln2,
=k(lnk-ln2)=f(k)-kln2,∴g(x)≥f(k)-kln2,
即f(x)+f(k-x)≥f(k)-kln2.令x=a,k-x=b,则k=a+b.∴f(a)+f(b)≥f(a+b)-(a+b)ln2.
∴f(a)+(a+b)ln2≥f(a+b)-f(b).
(文)解:
(1)∵f(x)=x
3+bx
2+cxz∴f′(x)=3x
2+2bx+c.
∵F(x)=f(x)+af′(x)=x3+(b+3a)x2+(c+2ab)x+ac为奇函数,由F(-x)=-F(x),可得b+3a=0,ac=0.
∵a>0,∴b=-3a,c=0.∴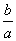 =-3,c=0.
=-3,c=0.
(2)由(1)可得f(x)=x3-3ax2,∴f′(x)=3x(x-2a).令3x(x-2a)≤0,解得0≤x≤2a.∴函数f(x)的单调递减区间为[0,2a].
(3)当a=2时,曲线y=f(x)在点A(t,f(t))处的切线方程为y-f(t)=f′(t)(x-t),kAB=f′(t)=3t(t-4).
联立方程组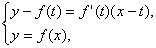 化简,得f(x)-f(t)=f′(t)(x-t),
化简,得f(x)-f(t)=f′(t)(x-t),
即x3-6x2-t3+6t2=(3t2-12t)(x-t),(x-t)(x2+xt+t2-6x-6t)=(x-t)(3t2-12t).
∵A、B不重合,∴x≠t.∴x2+xt+t2-6x-6t=3t2-12t.∴x2+(t-6)x-2t2+6t=0,
即(x-t)(x+2t-6)=0.∵x≠t,∴x=-2t+6.又另一交点为B(m,f(m)),∴m=-2t+6.
S(t)=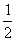 |m-t|·|f(m)-f(t)|=
|m-t|·|f(m)-f(t)|=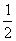 (m-t)2·|kAB|=
(m-t)2·|kAB|= (t-2)2·3t(4-t)=
(t-2)2·3t(4-t)=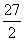 (t-2)2(4-t)t,其中t∈(0,2)∪(2,4).
(t-2)2(4-t)t,其中t∈(0,2)∪(2,4).
令h(t)=(t-2)2(4-t)t,其中t∈(0,2)∪(2,4).∵h(t)=-(t4-8t3+20t2-16t),
∴h′(t)=-4(t3-6t2+10t-4)=-4(t-2)(t-2+ )(t-2-
)(t-2-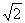 ).
).
由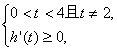 解得0<t≤2-
解得0<t≤2-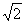 ,或2<t≤2+
,或2<t≤2+ .
.
于是函数h(t)在区间(0,2-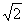 ]、(2,2+
]、(2,2+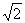 ]上是单调增函数;在区间[2-
]上是单调增函数;在区间[2-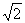 ,2)、[2+
,2)、[2+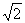 ,4)上是单调减函数.当t=2-
,4)上是单调减函数.当t=2- 和t=2+
和t=2+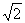 时,函数y=h(t)有极大值.
时,函数y=h(t)有极大值.
∴h(t)max=h(2-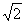 )=h(2+
)=h(2+ )=4.∴S(t)max=54.
)=4.∴S(t)max=54.
![]() (其中e=2.718 28…是自然对数的底数);
(其中e=2.718 28…是自然对数的底数);![]() 和c的值.
和c的值.
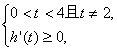 解得0<t≤2-
解得0<t≤2-