已知点A（1，1），B（1，﹣1），C（
cosθ， sinθ）（θ∈R），O为坐标原点．
（1）若|
|=
，求sin2θ的值；
（2）若实数m，n满足m
+n
=
，求（m﹣3）2+n2的最大值．
已知点A（1，1），B（1，﹣1），C（cosθ， sinθ）（θ∈R），O为坐标原点．
（1）若||=，求sin2θ的值；
（2）若实数m，n满足m+n=，求（m﹣3）2+n2的最大值．
【分析】（1）根据向量的坐标计算（终点坐标减始点坐标）求出
，然后再根据向量减法和模的坐标计算结合条件||=
得出sinθ+cosθ=
再两边平方即可得解．
（2）根据向量相等和条件m
+n
=
求出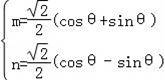
然后再代入（m﹣3）2+n2中可得（m﹣3）2+n2=﹣3（sinθ+cosθ）+10再结合辅助角公式可得（m﹣3）2+n2=﹣6sin（θ+
）+10从而可得出当sin（θ+）=﹣1时，（m﹣3）2+n2取得最大值16．
【解答】解：（1）∵|
﹣
|=|
|，A（1，1），B（1，﹣1），C（
cosθ， sinθ）
∴
=（
cosθ﹣1， sinθ﹣1）
∴|
|2=（
cosθ﹣1）2+（
sinθ﹣1）2=﹣2（sinθ+cosθ）+4．
∴﹣2（sinθ+cosθ）+4=2，即sinθ+cosθ=，
两边平方得1+sin2θ=
，
∴sin2θ=﹣．
（2）由已知得：（m，m）+（n，﹣n）=（cosθ， sinθ），
∴
解得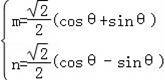
∴（m﹣3）2+n2=m2+n2﹣6m+9，
=﹣3（sinθ+cosθ）+10
=﹣6sin（θ+
）+10，
∴当sin（θ+）=﹣1时，（m﹣3）2+n2取得最大值16．