长度为
(>0)的线段AB的两个端点A、B分别在
轴和y轴上滑动，点P在线段AB上，且满足
(A为常数，且
)．
(1)求点P的轨迹方程C；
(2)当
时，过点M(1，0)作两条互相垂直的直线
和
，和分别与曲线C相交于点N和Q(N、Q都异于点M)，试问△MNQ能不能是等腰三角形?若能，请说明这样的三角形有几个；若不能，请说明理由．
长度为(>0)的线段AB的两个端点A、B分别在轴和y轴上滑动，点P在线段AB上，且满足(A为常数，且)．
(1)求点P的轨迹方程C；
(2)当时，过点M(1，0)作两条互相垂直的直线和，和分别与曲线C相交于点N和Q(N、Q都异于点M)，试问△MNQ能不能是等腰三角形?若能，请说明这样的三角形有几个；若不能，请说明理由．
解：(1)依题意，设点A、B的坐标分别为(
，0)、(0，
)，点P的坐标为(
)．
由
，得
)
=(
)．
∴
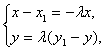即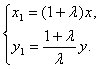
∵|AB|=
，∴
．
∴
，
∴点P的轨迹方程C是．
(2)当
时，曲线C的方程是
，故点M(1，0)在曲线C上．
依题意，可知直线
和
都不可能与坐标轴平行，可设直线方程为
，
直线方程为
，不妨设
．
由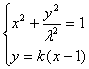
消去y得
．
由
，又
，得
，
∴
=
=
．
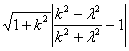
同理可得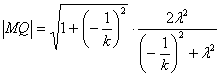
=
．
假设△MNQ是等腰三角形，则|MN|=|MQ|，
即
，
化简得
，
∴
或
①
①式的判别式△=
，
若△=
，解得
，此时①式无解；
若△==0，解得
，由①式得
=1；
若△=>0，解得
，由①式得
(可以验证≠1且>0)．
综上所述，△MNQ可以是等腰三角形，当0<
≤
时，这样的三角形有一个；
当时，这样的三角形有三个．