在平面直角坐标系xOy中，点A（5，0），对于某个正实数k，存在函数f（x）=ax2（a＞0），使得
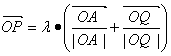（λ为常数），这里点P、Q的坐标分别为P（1，f（1）），Q（k，f（k）），则k的取值范围为（ ）
A、（2，+∞） B、（3，+∞） C、[4，+∞） D、[8，+∞）
在平面直角坐标系xOy中，点A（5，0），对于某个正实数k，存在函数f（x）=ax2（a＞0），使得
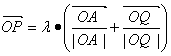（λ为常数），这里点P、Q的坐标分别为P（1，f（1）），Q（k，f（k）），则k的取值范围为（ ）
A、（2，+∞） B、（3，+∞） C、[4，+∞） D、[8，+∞）
解：由题设知，点P（1，a），Q（k，ak2），A（5，0），∴向量 
=（1，a）， 
=（5，0）， 
=（k，ak2），
∴ 
=（1，0）， 
=（ 
，
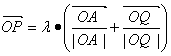），∵ （λ为常数），．
∴1=λ（1+ ），a= 
，两式相除得，k-1= 
，k-2=a2k＞0
∴k（1-a2）=2，且k＞2．∴k= 
，且0＜1-a2＜1．∴k= ＞2．故选A．