(本小题满分13分)
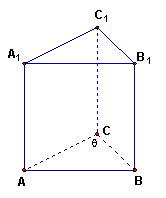 如图,在矩形木板
如图,在矩形木板![]() 中,
中,![]() ,
,![]() ,在二面角
,在二面角![]() 的墙角处围出一个侧棱与底面垂直的直三棱柱的储物仓,其中要求垂直于地面的木板两边与墙面贴紧。
的墙角处围出一个侧棱与底面垂直的直三棱柱的储物仓,其中要求垂直于地面的木板两边与墙面贴紧。
(Ⅰ)问应怎样围才能使储物仓的容积最大?并求出这个最大值?
(Ⅱ)在(Ⅰ)的条件下, 直线AB是否存在点P使得直线CP与平面![]() 所成角
所成角![]() ,若有则找出P点的位置;若不存在,请说明理由.
,若有则找出P点的位置;若不存在,请说明理由.
(本小题满分13分)
 如图,在矩形木板
如图,在矩形木板![]() 中,
中,![]() ,
,![]() ,在二面角
,在二面角![]() 的墙角处围出一个侧棱与底面垂直的直三棱柱的储物仓,其中要求垂直于地面的木板两边与墙面贴紧。
的墙角处围出一个侧棱与底面垂直的直三棱柱的储物仓,其中要求垂直于地面的木板两边与墙面贴紧。
(Ⅰ)问应怎样围才能使储物仓的容积最大?并求出这个最大值?
(Ⅱ)在(Ⅰ)的条件下, 直线AB是否存在点P使得直线CP与平面![]() 所成角
所成角![]() ,若有则找出P点的位置;若不存在,请说明理由.
,若有则找出P点的位置;若不存在,请说明理由.
(1)设![]() ,
,![]() ,则三棱柱体积
,则三棱柱体积![]() 。
。
又![]() ,
,![]()
![]() ,当且仅当
,当且仅当![]() 时,不等式取等号。
时,不等式取等号。
所以,当![]() 时,三棱柱体积
时,三棱柱体积![]()
(2)当![]() 时,
时,![]() 为等边三角形,取
为等边三角形,取![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则
![]() ,
,![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,
,![]() ;
;
![]() ,
,![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,则
,则
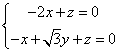 ,令
,令![]() ,得
,得![]() ;
;
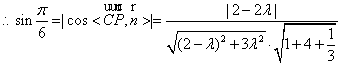 ,解得
,解得![]()
![]() 点在
点在![]() 的延长线上,且
的延长线上,且![]() ,使得直线CP与平面
,使得直线CP与平面![]() 所成角
所成角![]() 。
。