已知函数f(x)＝
．
（1）求f(x)的定义域及最小正周期； （2）求f(x)的单调递增区间．
已知函数f(x)＝．
（1）求f(x)的定义域及最小正周期； （2）求f(x)的单调递增区间．
解：（1）由sinx≠0得x≠kπ（k∈Z），故求f（x）的定义域为{x|x≠kπ，k∈Z}
∵f（x）=
=2cosx（sinx-cosx）
=sin2x-cos2x-1
=
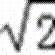sin（2x-
）-1
∴f（x）的最小正周期T=
=π。
（2）∵函数y=sinx的单调递减区间为[2kπ+
，2kπ+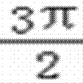
]（k∈Z）
∴由2kπ+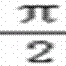
≤2x-
≤2kπ+
，x≠kπ（k∈Z）得kπ+
≤x≤kπ+
，（k∈Z）
∴f（x）的单调递减区间为：[kπ+
，kπ+
]（k∈Z）。