（07年崇文区一模理） 已知函数 （Ⅰ）求函数 （Ⅱ）求函数
处分别取得极值
的解析式；的单调区间与极值.
（07年崇文区一模理） 已知函数 （Ⅰ）求函数 （Ⅱ）求函数处分别取得极值的解析式；的单调区间与极值.
解析：（
.
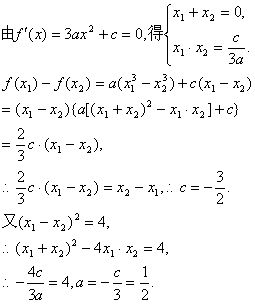
（II）
当
变化时，
的变化情况如下表：
|
| －1 | （－1，1） | 1 |
|
| + | 0 | － | 0 | + |
|
| 极大值1 |
| 极小值－1 |
|
由上表可知：
在区间
是增函数；
在区间（－1，1）上，
是减函数，
因此，当
有极大值为1；
当
有极小值为－1.
