首页 / 有人提出如下的圆周率的近似算法：在图3-2的单位正方形内均匀地取

有人提出如下的圆周率的近似算法：在图3-2的单位正方形内均匀地取

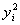
有人提出如下的圆周率的近似算法：在图3-2的单位正方形内均匀地取n个点Pi(xi,yi)(i∈{1,2,…,n}),然后统计出以xi,yi,1为边长的三角形中锐角三角形的个数m,则当n充分大时,π≈,试分析这种算法是否正确.

         图3-2

答案

解：

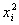
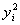
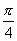
根据题中提出的算法,有0＜xi＜1,0＜yi＜1,所以以xi,yi,1为边长的三角形中,长为1的边所对角A为最大角,当且仅当0°＜A＜90°时,以xi,yi,1为边长的三角形为锐角三角形, +＞1,所以在图中的单位正方形内任意取一点Pi,满足以xi,yi,1为边长的三角形为锐角三角形的概率为P=阴影部分的面积/单位正方形的面积=1-,当n充分大时,mn≈P=1-,

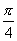
所以π≈4(1-)=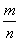

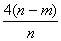
所以题中给出的圆周率的近似算法是正确的.

相关题目

羽扇纶巾，谈笑间，                  。（苏轼《念
羽扇纶巾，谈笑间，                  。（苏轼《念奴娇·赤壁怀古》）
19．描写小人物是欧∙亨利小说中最令人注目的内容。他的作
19．描写小人物是欧∙亨利小说中最令人注目的内容。他的作品往往描写了大都市里小人物的不幸命运和美好的品质，请你以《麦琪的礼物》或者其他的
关于图-1中各装置的叙述不正确的是        （     ）A
关于图-1中各装置的叙述不正确的是        （     ）A．装置①能验证AgCl沉淀可转化为溶解度更小的Ag2S沉淀B．装置②中X若为四氯化碳，可用于吸
下列现象的产生主要与太阳活动有关的是（    ） ①昼夜交
下列现象的产生主要与太阳活动有关的是（    ） ①昼夜交替    ②无线电短波通讯出现短暂的中断    ③狮子座流星雨    ④手表上的指南针指
读“气温变化图”，完成以下问题。   1．造成图示现象的
读“气温变化图”，完成以下问题。   1．造成图示现象的根本原因是( ) A．大气中的臭氧含量增加               B．大气中二氧化碳含量的增
已知，则（    ） A.                   B.       
已知，则（    ） A.                   B.                   C.                 D.
---Is that building a library?    ---__________.    A. Yes, there is 
---Is that building a library?    ---__________.    A. Yes, there is   B. Yes, it isn’t   C. No, there isn’t    D. No, it isn’t
《中国农业现代化道路的探索》指出：“它将家庭经营引入
《中国农业现代化道路的探索》指出：“它将家庭经营引入集体经济组织内部，家庭经营只是其中一个层次，统和分是相互依存、相互促进、共同发展

最新题目

下列各句中，没有语病的一句是（     ） A．当代中国来说
轮船是采用          的办法增大可以利用的浮力；而潜
为了防止希腊债务危机蔓延对欧元产生负面影响，2010年5月10
下列说法不符合ⅦA族元素性质特征的是       （    ）A
下面是某学生向老师祝寿时发言的一个片段，其中有四处不
下列叙述错误的是（ ） A．生铁中含有碳，抗腐蚀能力比纯
德国是一个能引发后人无限思考的国家。某班准备开展历史
第二次工业革命促使资本主义生产关系发生重大变化。这种
如图，折叠矩形纸片ABCD，使点B落在边AD上，折痕EF的两端分
下列各组词语中读音和书写有错误的一项是（3分）A．心无旁
去年暑假期间，张明与同学结伴去重庆旅游，他一路享受的
某历史研究小组在探究“影视材料中的历史”时发现，电视
下列各式不正确的是(    ) A.终边在x轴上角的集合是{α|α=kπ
下图为某电场中的一条电场线，针对电场线上A、B两点的场强
方程的根是                 。
名著阅读。（6分） （1）下面对名著内容表述不正确的一项
通过观察下述两等式的规律，请你写出一个(包含下面两命题)
将分子、原子、离子、质子、中子和电子分别填入下列空格
 当地时间2011年2月22日中午12时51分，新西兰第三大城市克莱
阅读【甲】【乙】两段文言文，完成后面题目。（13分）【甲