如图,在矩形![]() 中,
中,![]() .将
.将![]() 向内翻折,点
向内翻折,点![]() 落在
落在![]() 上,记为
上,记为![]() ,折痕为
,折痕为![]() .若将
.若将![]() 沿
沿![]() 向内翻折,点
向内翻折,点![]() 恰好落在
恰好落在![]() 上,记为
上,记为![]() ,则
,则![]() _____.
_____.
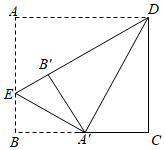
如图,在矩形![]() 中,
中,![]() .将
.将![]() 向内翻折,点
向内翻折,点![]() 落在
落在![]() 上,记为
上,记为![]() ,折痕为
,折痕为![]() .若将
.若将![]() 沿
沿![]() 向内翻折,点
向内翻折,点![]() 恰好落在
恰好落在![]() 上,记为
上,记为![]() ,则
,则![]() _____.
_____.

![]() .
.
【分析】
利用矩形的性质,证明![]() ,
,![]() ,推出
,推出![]() ,
,![]() ,设
,设![]() ,在
,在![]() 中,通过勾股定理可求出
中,通过勾股定理可求出![]() 的长度.
的长度.
【详解】
∵四边形![]() 为矩形,
为矩形,
∴![]() ,
,![]() ,
,
由翻折知,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,
![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴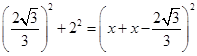 ,
,
解得,![]() (负值舍去),
(负值舍去),![]() ,
,
故答案为![]() .
.
【点睛】
本题考查了矩形的性质,轴对称的性质,解直角三角形等知识,解题关键是通过轴对称的性质证明![]() .
.