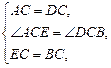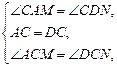已知：如图，△DAC、△EBC均是等边三角形，点A、C、B在同一条直线上
已知：如图，△DAC、△EBC均是等边三角形，点A、C、B在同一条直线上，且AE、BD分别与CD、CE交于点M、N.
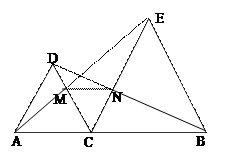
求证：（1）AE=DB；
（2）△CMN为等边三角形.
证明略解析:
证明：(1)∵△
DAC、△
EBC均是等边三角形，
∴
AC＝
DC，
EC＝
BC，∠
ACD＝∠
BCE＝60°，………… 2分
∴∠
ACD+∠
DCE＝∠
BCE+∠
DCE，
即∠
ACE＝∠
DCB． ……………… 3分
在△
ACE和△
DCB中，
∴△
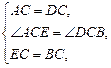
ACE≌△
DCB(SAS)． ………… 5分
∴
AE＝
DB． ……………… 6分
(2)由(1)可知：△
ACE≌△
DCB，
∴∠
CAE＝∠
CDB，
即∠
CAM＝∠
CDN． ……………… 7分
∵△
DAC、△
EBC均是等边三角形，
∴
AC＝
DC，∠
ACM＝∠
BCE＝60°．
又点
A、
C、
B在同一条直线上，
∴∠
DCE＝180°－∠
ACD－∠
BCE＝180°－60°－60°＝60°，
即∠
DCN＝60°．
∴∠
ACM＝∠
DCN． ………… 8分
在△
ACM和△
DCN中，
∴△
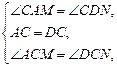
ACM≌△
DCN(ASA)． ……………… 10分
∴
CM＝
CN． ……………… 11分
又∠
DCN＝60°，
∴△
CMN为等边三角形． ……………12分
