·
=0,又
=-
.(1)当点P在y轴上移动时,求点M的轨迹C的方程;
(2)若直线l:y=k(x-1)(k＞2)与轨迹C交于A、B两点,AB中点N到直线3x+4y+m=0(m＞-3)的距离为
,求m的取值范围.
·=0,又=-.(1)当点P在y轴上移动时,求点M的轨迹C的方程;
(2)若直线l:y=k(x-1)(k＞2)与轨迹C交于A、B两点,AB中点N到直线3x+4y+m=0(m＞-3)的距离为,求m的取值范围.
解:(1)设M(x,y).由=-,得P(0,-),Q(,0).
由·
=0
(3,-
)·(x,
y)=0
y2=4x(x＞0).
(2)联立y=k(x-1)(k＞2)与y2=4x,
消去y,得k2x2-2(k2+2)x+k2=0.
由N是AB中点N(
,
).
又由已知
=
|
+
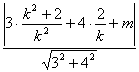+m+3|=1.
∵k＞2,m＞-3,∴
+
+m+3=1.
令
=t,则0＜t＜
.
又m=-6t2-8t-2
-
＜m＜-2.
结合m＞-3,∴-3＜m＜-2.