已知一张矩形纸片OACB，将该纸片放置在平面直角坐标系中，点A（11，0），B（0，6），点P为BC边上的动点（点P不与点B，C重合），经过点O、P折叠该纸片，得点B′和折痕OP．设BP＝t 。
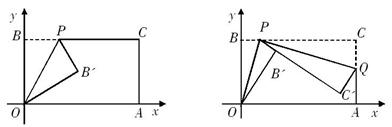
（1）如图①，当∠BOP＝30°时，求点P的坐标；
（2）如图②，经过点P再次折叠纸片，使点C 落在直线PB′上，得点C′和折痕PQ，若AQ＝m，试用含有t的式子表示m；
（3）在（2）的条件下，当点C′恰好落在边OA上时，求点P的坐标。（直接写出结果即可）
|
已知一张矩形纸片OACB，将该纸片放置在平面直角坐标系中，点A（11，0），B（0，6），点P为BC边上的动点（点P不与点B，C重合），经过点O、P折叠该纸片，得点B′和折痕OP．设BP＝t 。
（1）如图①，当∠BOP＝30°时，求点P的坐标；
（2）如图②，经过点P再次折叠纸片，使点C 落在直线PB′上，得点C′和折痕PQ，若AQ＝m，试用含有t的式子表示m；
（3）在（2）的条件下，当点C′恰好落在边OA上时，求点P的坐标。（直接写出结果即可）
|
解：（1）根据题意，有∠OBP = 90°，OB = 6，
在Rt△OBP中，由∠BOP = 30°，BP =t，得OP＝2t.
∵OP 2 ＝ OB 2+BP 2，即（2t）2 ＝62+t 2，解得t1＝
，t2＝－（舍去）．
∴点P的坐标为（ ，6）．
（2）∵△OB′P，△QC′P分别是由△OBP，△QCP折叠得到的，
∴△OB′P ≌ △OBP，△QC′P ≌ △QCP.
∴∠OPB′＝∠OPB，∠QPC′＝∠QPC.
∵∠OPB′+∠OPB +∠QPC′+∠QPC＝180°，∴∠OPB +∠QPC＝90°.
∵∠BOP +∠OPB＝90°，∴∠BOP＝∠CPQ.
又∵∠OBP＝∠C = 90°，∴△OBP∽△PCQ.∴
.
由题意知，BP＝t，AQ＝m，BC＝11，AC＝6，则PC＝11－t，CQ＝6－m．
∴
∴
（0＜t＜11）.
（3）点P的坐标为（
，6）或（
，6）.