在直角梯形OABC中，CB//OA，ÐCOA=90°，CB=3，OA=6，BA=3。分别以OA、OC边

 在直角梯形OABC中，CB//OA，ÐCOA=90°，CB=3，OA=6，BA=3。分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系。

   (1) 求点B的坐标；

   (2) 已知D、E分别为线段OC、OB上的点，OD=5，OE=2EB，直线DE交x轴于点F。求直线DE的解析      式；

   (3) 点M是(2)中直线DE上的一个动点，在x轴上方的平面内是否存在另一个点N，使以O、D、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由。

 [解] (1) 如图1，作BH^x轴于点H，则四边形OHBC为矩形，

       ∴OH=CB=3，∴AH=OA-OH=6-3=3，

     在Rt△ABH中，BH===6，

  ∴点B的坐标为(3，6)

 (2) 如图1，作EG^x轴于点G，则EG//BH，

∴△OEG~△OBH，∴== ，又∵OE=2EB，

 ∴=，∴==，∴OG=2，EG=4，∴点E的坐标为(2，4)。

          又∵点D的坐标为(0，5)，设直线DE的解析式为y=kx+b，则，解得k= -，

          b=5。∴直线DE的解析式为：y= -x+5。

       (3) 答：存在。

          j 如图1，当OD=DM=MN=NO=5时，四边形ODMN为菱形。作MP^y轴于点P，

             则MP//x轴，∴△MPD~△FOD，∴==。

             又∵当y=0时，-x+5=0，解得x=10。∴F点的坐标为(10，0)，∴OF=10。

             在Rt△ODF中，FD===5，∴==，

             ∴MP=2，PD=。∴点M的坐标为(-2，5+)。

             ∴点N的坐标为(-2，)。

          k 如图2，当OD=DN=NM=MO=5时，四边形ODNM

             为菱形。延长NM交x轴于点P，则MP^x轴。

             ∵点M在直线y= -x+5上，∴设M点坐标为

             (a，-a+5)，在Rt△OPM中，OP 2+PM 2=OM 2，

             ∴a2+(-a+5)2=52，解得a1=4，a2=0(舍去)，

             ∴点M的坐标为(4，3)，∴点N的坐标为(4，8)。

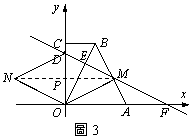
     l 如图3，当OM=MD=DN=NO时，四边形OMDN为

        菱形。连接NM，交OD于点P，则NM与OD互相

        垂直平分，∴yM=yN=OP=，∴-xM+5=，∴xM=5，

        ∴xN= -xM= -5，∴点N的坐标为(-5，)。

     综上所述，x轴上方的点N有三个，分别为N1(-2，)，

               N2(4，8)，N3(-5，)。