若双曲线
-
=1的一条渐近线被圆(x-2)2+y2=4所截得的弦长为2，则该双曲线的实轴长为 .
若双曲线-=1的一条渐近线被圆(x-2)2+y2=4所截得的弦长为2，则该双曲线的实轴长为 .
2
双曲线的一条渐近线为
x-ay=0，圆的半径r=2，圆心到渐近线的距离为d=
，依题意有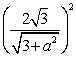
+1=4，解得a=1，所以双曲线的实轴长为2a=2.
【精要点评】对于双曲线的几何性质，考查较多的是双曲线的离心率、渐近线.求离心率或离心率的取值范围常用的方法是依据条件列出关于a，c的齐次方程或不等式，再转化为关于e的方程或不等式求解.求双曲线的渐近线要分清两种情况下的双曲线所对应的渐近线方程.