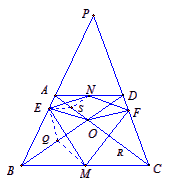
给定锐角三角形PBC，
．设A，D分别是边PB，PC上的点，连接AC，BD，相交于点O. 过点O分别作OE⊥AB，OF⊥CD，垂足分别为E，F，线段BC，AD的中点分别为M，N．
（1）若A，B，C，D四点共圆，求证：
；
（2）若 ，是否一定有A，B，C，D四点共圆？证明你的结论．
给定锐角三角形PBC，．设A，D分别是边PB，PC上的点，连接AC，BD，相交于点O. 过点O分别作OE⊥AB，OF⊥CD，垂足分别为E，F，线段BC，AD的中点分别为M，N．
（1）若A，B，C，D四点共圆，求证：；
（2）若 ，是否一定有A，B，C，D四点共圆？证明你的结论．
见解析
（1）设Q，R分别是OB，OC的中点，连接EQ，MQ，FR，MR，则
，
又OQMR是平行四边形，
所以
，
由题设A，B，C，D四点共圆，
所以
， 
于是
，
所以
，
故 
，
所以 EM＝FM，
同理可得 EN＝FN，
所以 
．
（2）答案是否定的．
当AD∥BC时，由于
，所以A，B，C，D四点不共圆，但此时仍然有，证明如下：
如图2所示，设S，Q分别是OA，OB的中点，连接ES，EQ，MQ，NS，则
，
所以 
． ①
又
，
所以
． ②
而AD∥BC，所以
， ③
由①，②，③得 
．
因为 
，
，
即
，
所以
～
， 
故 
（由②）．
同理可得， 
，
所以 
，
从而 ．