(本题满分16分) 本题共有3个小题,第1小题满分4分,第2小题满分4分,第3小题满分8分.
设![]() 是等差数列,
是等差数列,![]() 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的通项公式;
的通项公式;
(2)记![]() ,
,![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,当
项和,当![]() 为多少时
为多少时![]() 取得最大值或最小值?
取得最大值或最小值?
(3)是否存在正数![]() ,使得
,使得![]() 对一切
对一切![]() 均成立,若存在,求出
均成立,若存在,求出![]() 的最大值,若不存在,说明理由.
的最大值,若不存在,说明理由.
(本题满分16分) 本题共有3个小题,第1小题满分4分,第2小题满分4分,第3小题满分8分.
设![]() 是等差数列,
是等差数列,![]() 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的通项公式;
的通项公式;
(2)记![]() ,
,![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,当
项和,当![]() 为多少时
为多少时![]() 取得最大值或最小值?
取得最大值或最小值?
(3)是否存在正数![]() ,使得
,使得![]() 对一切
对一切![]() 均成立,若存在,求出
均成立,若存在,求出![]() 的最大值,若不存在,说明理由.
的最大值,若不存在,说明理由.
解:
(1)设![]() 的公差为
的公差为![]() ,
,![]() 的公比为
的公比为![]() ,则依题意有
,则依题意有![]() 且
且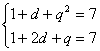
解得![]() ,
,![]() . …………………………………………………………………………2分
. …………………………………………………………………………2分
所以![]() ,
,![]() .…………………………………………2分
.…………………………………………2分
(2)因为![]()
![]() ,所以,当
,所以,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .……………………………………………………………………………………2分
.……………………………………………………………………………………2分
所以当![]() 时,
时,![]() 取得最小值. ……………………………………………………2分
取得最小值. ……………………………………………………2分
(文)(3)![]() .
.![]() ① ………………………2分
① ………………………2分
![]() ②
②
②-①得![]() …………………………………………………2分
…………………………………………………2分
![]()
 ……………………………3分
……………………………3分
![]() .……………………………………………………………………………………………1分
.……………………………………………………………………………………………1分
(理)(3)![]() 等价于
等价于![]() ,
,
其中![]() ;……………………………………2分
;……………………………………2分
因为:![]()
![]()
![]()
![]()
![]() 显然成立,所以
显然成立,所以![]() 是递增的。……………4分
是递增的。……………4分
从而![]() . …………………………………………………………2分
. …………………………………………………………2分
或因为: ![]() ,所以:
,所以:![]() 是递增的。………………………4分; 从而
是递增的。………………………4分; 从而![]() .………………………………2分
.………………………………2分