直角
的外接圆圆心O，半径为1，且
，则向量
在向量
方向的投影为（ ）
A. 
B. 
C. 
D. 
直角的外接圆圆心O，半径为1，且，则向量在向量方向的投影为（ ）
A. B. C. D.
A
【解析】
【分析】
根据题意求得，三角形的外心O点在BC的中点处，且∠ABC=
，由向量投影的定义，利用已知条件求出即可．
【详解】直角
外接圆圆心O落在BC的中点上，
根据题意画出图像，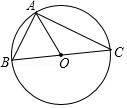
又O为△ABC外接圆的圆心，半径为1，
∴BC为直径，且BC=2，OA=AB=1，∠ABC=；
∴向量在向量方向的投影
|cos=
．
故选：A．
【点睛】此题主要考查了向量投影的概念与直角三角形外接圆的性质应用问题，是基础题．解决向量的小题常用方法有：数形结合，向量的三角形法则，平行四边形法则等；建系将向量坐标化；向量基底化，选基底时一般选择已知大小和方向的向量为基底。