如图所示，在空间四边形ABCD中，AD＝BC＝2，E，F分别是AB，CD的中点．若EF＝
，求AD，
BC所成的角．
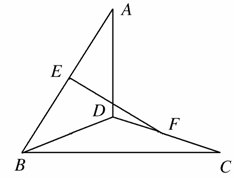
如图所示，在空间四边形ABCD中，AD＝BC＝2，E，F分别是AB，CD的中点．若EF＝，求AD，BC所成的角．
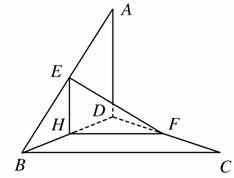
解 取BD的中点H，连接EH，FH，因为E是AB的中点，且AD＝2，∴EH∥AD，EH＝1.
同理FH∥BC，FH＝1，
∴∠EHF是异面直线AD，BC所成的角，又因为EF＝，
∴△EFH是等腰直角三角形，EF是斜边
，
∴∠EHF＝90°，即AD，BC所成的角是90°.