如图所示,遥控电动赛车(可视为质点)从A点由静止出发,经过时间t后关

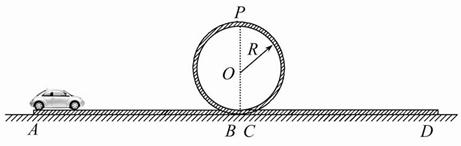
如图所示,遥控电动赛车(可视为质点)从A点由静止出发,经过时间t后关闭电动机,赛车继续前进至B点后进入固定在竖直平面内的圆形光滑轨道,通过轨道最高点P后又进入水平轨道CD上。已知赛车在水平轨道AB部分和CD部分运动时受到的阻力恒为车重的0.5倍,即k==0.5,赛车的质量m=0.4 kg,通电后赛车的电动机以额定功率P=2 W工作,轨道AB的长度L=2 m,圆形轨道的半径R=0.5 m,空气阻力可以忽略,取重力加速度g=10 m/s²。某次比赛,要求赛车在运动过程中既不能脱离轨道,又要在CD轨道上运动的路程最短。在此条件下,求:

 (1)赛车在CD轨道上运动的最短路程；

(2)赛车电动机工作的时间。

【解析】(1)要求赛车在运动过程中既不能脱离轨道,又在CD轨道上运动的路程最短,则赛车经过圆轨道P点时速度最小,此时赛车对轨道的压力为零,重力提供向心力:

mg=                                                                       (3分)

赛车在C点的速度为v_C,由机械能守恒定律可得:

mg·2R+                                                     (3分)

由上述两式联立，代入数据可得：v_C=5 m/s                              (1分)

设赛车在CD轨道上运动的最短路程为x,由动能定理可得：

                                                             (3分)

代入数据可得：x=2.5 m                                                   (1分)

(2)由于竖直圆轨道光滑，由机械能守恒定律可知：

v_B=v_C=5 m/s

从A点到B点的运动过程中，由能量守恒定律可得：

Pt=kmgL+                                                             (3分)

代入数据可得：t=4.5 s                                                   (2分)

答案：(1)2.5 m      (2)4.5 s

【总结提升】与功能关系相结合的圆周运动问题的分析方法

(1)确定研究对象，对研究对象进行受力分析和做功情况分析，对于多个过程的情形，要分析出在每一个过程中的受力和做功情况。

(2)注意不同过程的衔接,前一个过程的末状态,就是后一个过程的初状态。

(3)分析每一个过程中的能量转化情况,机械能是否守恒,列出每一个过程的对应方程。

(4)确定临界状态及特点,并列出相应的方程。

(5)求解方程并进行验证。