如图甲所示，质量为m＝1kg的物体置于倾角为θ＝37°的固定且足够长的斜面上，对物体施以平行于斜面向上的拉力F，t1＝0.5s时撤去拉力，物体速度与时间（v—t）的部分图像如图乙所示。（g=10m/s2 ，sin37°＝0.6，cos37°＝0.8）问：
（1）物体与斜面间的动摩擦因数μ为多少？
（2）拉力F的大小为多少？
（3）物体沿斜面向上滑行的最大距离s为多少？
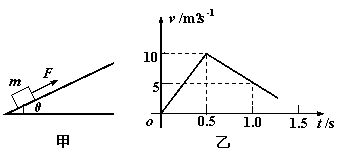
如图甲所示，质量为m＝1kg的物体置于倾角为θ＝37°的固定且足够长的斜面上，对物体施以平行于斜面向上的拉力F，t1＝0.5s时撤去拉力，物体速度与时间（v—t）的部分图像如图乙所示。（g=10m/s2 ，sin37°＝0.6，cos37°＝0.8）问：
（1）物体与斜面间的动摩擦因数μ为多少？
（2）拉力F的大小为多少？
（3）物体沿斜面向上滑行的最大距离s为多少？
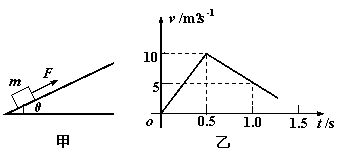
解：（1）设物体在力F作用时的加速度为a1，撤去力F后物体的加速度大小为a2，
根据图像可知：
① （1分）
② （1分）
撤去力F 后对物体进行受力分析，由牛顿第二定律可知
mgsinθ＋μmgcosθ＝ma2 ③ （1分）
解得：
④ （1分）
（2）在力F作用时对物体进行受力分析，由牛顿第二定律可知
F－mgsinθ－μmgcosθ＝ma1 ⑤ （1分）
F=m(a1+gsinθ+μgcosθ)=1×(20+10×0.6+0.5×10×0.8)N=30N ⑥ （1分）
（3）设撤去力F后物体运动到最高点所花时间为t2，此时物体速度为零，有
0=v1－a2t2，
得 t2＝1s ⑦ （2分）
向上滑行的最大距离：
⑧ （2分）
【得出⑦式后，也可根据v-t图像中图线所围面积求得向上滑行的最大距离：
s=
⑧ （2分） 】