（本小题满分14分）
设
、
是函数
的两个极值点。
（1）若
，求函数
的解析式；
（2）若
，求
的最大值。
（3）若
，且
，函数
，
求证：
（本小题满分14分）
设、是函数的两个极值点。
（1）若，求函数的解析式；
（2）若，求的最大值。
（3）若，且，函数，
求证：
（本小题满分14分）
解：
…………1分
（1）∵
是函数
的两个极值点，
∴
，
。……………………………………………………2分
∴
，
，解得
。………………3分
∴
。…………………………………………………………4分
（2）∵
是函数的两个极值点，∴
。
∴是方程
的两根。
∵
，∴
对一切
恒成立。
，
，
∵
，∴
。
∴
。……………………6分
由
得
，∴
。…………7分
∵
，∴
，∴
。……………………………………8分
令
，则
。
当
时，
，∴
在（0，4）内是增函数；
当
时，
，∴在（4，6）内是减函数。……………………9分
∴当
时，有极大值为96，∴在
上的最大值是96，
∴
的最大值是
。………………………………………………………………10分
（3）证法一：∵是方程
的两根，
∴
，……………………………………………………11分
∴
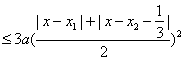………………12分
∵
，∴
，
，
∴
。
∵，
，∴
。
∴
。……………………………………14分
证法二：∵是方程的两根，
∴，……………………………………………………11分
∵，，∴。
∴
∵，
∴
………………………………………………12分
。………………………………………………14分