若数列![]() 是各项均不为
是各项均不为![]() 的等差数列,公差为
的等差数列,公差为![]() ,
,![]() 为其前
为其前![]() 项和,且满足
项和,且满足![]() ,
,![]() .数列
.数列![]() 满足
满足![]() ,
,![]() 为数列
为数列![]() 的前n项和.
的前n项和.
(1)求![]() 、
、![]() 和
和![]() ;
;
(2)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)是否存在正整数![]()
![]() ,使得
,使得![]() 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
若数列![]() 是各项均不为
是各项均不为![]() 的等差数列,公差为
的等差数列,公差为![]() ,
,![]() 为其前
为其前![]() 项和,且满足
项和,且满足![]() ,
,![]() .数列
.数列![]() 满足
满足![]() ,
,![]() 为数列
为数列![]() 的前n项和.
的前n项和.
(1)求![]() 、
、![]() 和
和![]() ;
;
(2)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)是否存在正整数![]()
![]() ,使得
,使得![]() 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
解:(1)(法一)在![]() 中,令
中,令![]() ,
,![]() ,
,
得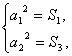 即
即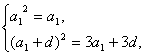 解得
解得![]() ,
,![]() ,
,![]() .
.
![]() ,
,
![]() .
.
(法二)![]()
![]() 是等差数列,
是等差数列, ![]()
![]()
![]() .由
.由![]() ,得
,得 ![]() ,
,
又![]() ,
,![]() ,则
,则![]() .(
.(![]() 求法同法一)
求法同法一)
(2)①当![]() 为偶数时,要使不等式
为偶数时,要使不等式![]() 恒成立,即需不等式
恒成立,即需不等式![]() 恒成立.
恒成立.
![]() ,等号在
,等号在![]() 时取得.
时取得.![]() 此时
此时![]() 需满足
需满足![]() .
.
②当![]() 为奇数时,要使不等式
为奇数时,要使不等式![]() 恒成立,
恒成立,
即需不等式![]() 恒成立.
恒成立.
![]() 是随
是随![]() 的增大而增大,
的增大而增大, ![]() 时
时![]() 取得最小值
取得最小值![]() .
.
![]() 此时
此时![]() 需满足
需满足![]() .综合①、②可得
.综合①、②可得![]() 的取值范围是
的取值范围是![]() .
.
(3)![]() ,
,
若![]() 成等比数列,则
成等比数列,则![]() ,即
,即![]() .
.
(法一)由![]() , 可得
, 可得![]() ,
,
即![]() ,
,![]()
![]() .
.
又![]() ,且
,且![]() ,所以
,所以![]() ,此时
,此时![]() .
.
因此,当且仅当![]() ,
, ![]() 时,数列
时,数列![]() 中的
中的![]() 成等比数列.
成等比数列.
(法二)因为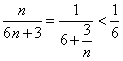 ,故
,故![]() ,即
,即![]() ,
,
![]()
![]() ,(以下同上).
,(以下同上).