如图，△ABC中,∠A＝60°,P为AB上一点， Q为BC延长线上一点，且PA=CQ，连PQ交AC边于D, PD=DQ,证明：△ABC为等边三角形.
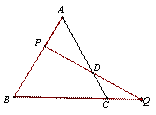
如图，△ABC中,∠A＝60°,P为AB上一点， Q为BC延长线上一点，且PA=CQ，连PQ交AC边于D, PD=DQ,证明：△ABC为等边三角形.
证明：过P作PE∥BQ交AC于E
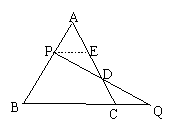∴∠EPD=∠Q
在△EPD和△CQD中
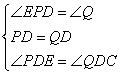
∴△EPD≌△CQD（ASA）
∴PE=CQ，∵PA=CQ，∴PE=PA，∴∠PEA=∠A=60°
∵PE∥BQ，∴∠PEA=∠ACB=60°∴∠A=∠ACB=∠B=60°
∴△ABC为等边三角形