,
=2
,求以直线OP1、OP2为渐近线且过点P的离心率为
的双曲线方程. 
,=2,求以直线OP1、OP2为渐近线且过点P的离心率为的双曲线方程.
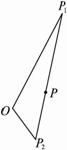
解:以O为原点，∠P1OP2的平分线为x轴建立直角坐标系，设双曲线的方程为
,由于双曲线的离心率为，∴e2=.
∴.∴两条渐近线的方程为y=±x.
由此设点P1(x1,
x1),P2(x2,-
x2)(x1＞0,x2＞0),由题设知点P分P1P2所成的比λ=2,得点P的坐标为(
,
),又点P在双曲线上，
∴
-
=1,即(x1+2x2)2-(x1-2x2)2=
又|OP1|=
=
x1, |OP2|=
x2且sin∠P1OP2=
.
∴S△=
|OP1||OP2|sin∠P1OP2=
×
x1x2×
=
,由此得x1x2=
.代入①式得a2=4,
∴b2=9,所求方程为
.