已知A、B为抛物线C:y2 = 4x上的两个动点,点A在第一象限,点B在第四象限l1、l2分别过点A、B且与抛物线C相切,P为l1、l2的交点.
(Ⅰ)若直线AB过抛物线C的焦点F,求证:动点P在一条定直线上,并求此直线方程;
(Ⅱ)设C、D为直线l1、l2与直线x = 4的交点,求![]() 面积的最小值.
面积的最小值.
已知A、B为抛物线C:y2 = 4x上的两个动点,点A在第一象限,点B在第四象限l1、l2分别过点A、B且与抛物线C相切,P为l1、l2的交点.
(Ⅰ)若直线AB过抛物线C的焦点F,求证:动点P在一条定直线上,并求此直线方程;
(Ⅱ)设C、D为直线l1、l2与直线x = 4的交点,求![]() 面积的最小值.
面积的最小值.
【解析】(Ⅰ)设![]() ,
, ![]() (
(![]() ).
).
易知![]() 斜率存在,设为
斜率存在,设为![]() ,则
,则![]() 方程为
方程为![]() .
.
由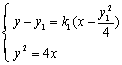 得,
得,![]() …………… ①
…………… ①
由直线![]() 与抛物线
与抛物线![]() 相切,知
相切,知![]() .
.
于是,![]() ,
,![]() 方程为
方程为![]() .
.
同理,![]() 方程为
方程为![]() .
.
联立![]() 、
、![]() 方程可得点
方程可得点![]() 坐标为
坐标为![]() ,
,
∵ 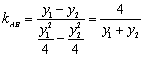 ,
,![]() 方程为
方程为![]() ,
,
![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() .
.
 ∴
∴ 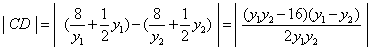 .
.
∴ ![]() .
.
设![]() (
(![]() ),
),![]() ,
,
由![]() 知,
知,![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
∴ ![]() .
.
设![]() ,则
,则![]() .
.
∴ ![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.![]() 在区间
在区间![]() 上为减函数;
上为减函数;
在区间![]() 上为增函数.
上为增函数.
∴ ![]() 时,
时,![]() 取最小值
取最小值![]() .
.
∴ 当![]() ,
,![]() ,
,
即![]() ,
,![]() 时,
时,![]() 面积取最小值
面积取最小值![]() . ………… 13分
. ………… 13分