解法一：设A（y12，y1），B（y22，y2），则
y2-y1=1
(y12-y22)2+(y1-y2)2=(
将①式代入②,得（y12-1+2y1-y12）2+（y1-1+y1）2=
化简,得4(2y1-1)2=(y1-y12-4)2.
∴4y1-2=y1-y12-4.∴y1=-2或y1=-1.
∴|AB|=
,∴S=|AB|2=50或18.解法二：设A(y02,y0),ABCD边长为d,由于AC平行于y轴,且|AC|=
d),且B(y02+
d,y0+
d).于是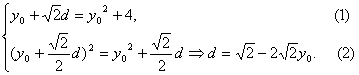
∴y0=-2或-1，∴|AB|=
.∴S=|AB|2=50或18.
解法三：如下图所示，设ABCD的边长为d，则直线AB的方程为y=x+4-
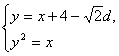消去x，得y2-y+4-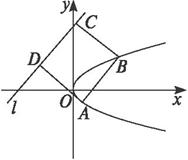
d=0.
由韦达定理,得y1+y2=1，y1y2=4-
又∵|AB|=d-
，∴2［12-4（4-
d+30=0，解之，得d=3
或d=5
.∴正方形面积为18或50.
深化升华
从三个解法中可体会到，所设未知数不同.列方程的依据就不同,解答过程的繁简就不一样.应特别注意参数的设法，合理利用图形的特点以化简运算.