如图,在△ABC中,AB=AC,D是BC中点,AE平分∠BAD交BC于点E,点O是AB上一点,⊙O过A、E两点, 交AD于点G,交AB于点F.
(1)求证:BC与⊙O相切;
(2)当∠BAC=120°时,求∠EFG的度数.
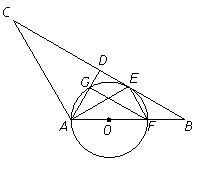

如图,在△ABC中,AB=AC,D是BC中点,AE平分∠BAD交BC于点E,点O是AB上一点,⊙O过A、E两点, 交AD于点G,交AB于点F.
(1)求证:BC与⊙O相切;
(2)当∠BAC=120°时,求∠EFG的度数.


(1)证明:连接OE,


∵AB=AC且D是BC中点,∴AD⊥BC.
∵AE平分∠BAD,∴∠BAE=∠DAE.
∵OA=OE,∴∠OAE=∠OEA.∴∠OEA=∠DAE.
∴OE∥AD.∴OE⊥BC.∴BC是⊙O的切线.
(2)∵AB=AC,∠BAC=120°,∴∠B=∠C=30°.∴∠EOB =60°.
∴∠EAO =∠EAG =30°.∴∠EFG =30°.