以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B两点,求线段AB的最小值.
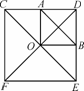
以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B两点,求线段AB的最小值.

∵四边形CDEF是正方形,
∴∠OCD=∠ODB=45°,∠COD=90°,OC=OD.
∵AO⊥OB,
∴∠AOB=90°.
∴∠AOC+∠AOD=90°,∠AOD+∠BOD=90°.
∴∠AOC=∠BOD.
∵在△COA和△DOB中,
∴△COA≌△DOB.
∴OA=OB.
∵∠AOB=90°,
∴△AOB是等腰直角三角形.
由勾股定理得AB=![]() =
=![]() OA,
OA,
要使AB最小,只要OA取最小值即可,
根据垂线段最短,OA⊥CD时,OA最小,
∵四边形CDEF是正方形,
∴FC⊥CD,OD=OF=OC.
∴CA=DA.
∴OA=![]() CF=1.
CF=1.
∴AB=![]() .
.
∴AB的最小值为![]() .
.