(1)求数列{an}的通项公式;
(2)设数列{bn}的前n项和为Tn,且bn=
,求证:对任意正整数n,总有Tn＜2;
(3)在正数数列{cn}中,设(cn)n+1=
an+1(n∈N
(文)已知数列{xn}满足xn+1-xn=(
)n,n∈N
xn
,且T2n=a1+2a2+3a3+…+ (2n-1)a2n-1+2na2n.(1)求xn的表达式;
(2)求T2n;
(3)若Qn=1
(n∈N
(1)求数列{an}的通项公式;
(2)设数列{bn}的前n项和为Tn,且bn=,求证:对任意正整数n,总有Tn＜2;
(3)在正数数列{cn}中,设(cn)n+1=an+1(n∈N
(文)已知数列{xn}满足xn+1-xn=()n,n∈N
xn,且T2n=a1+2a2+3a3+…+ (2n-1)a2n-1+2na2n.(1)求xn的表达式;
(2)求T2n;
(3)若Qn=1(n∈N
(理)(1)解：
∵Sn=2an-2(n∈N*), ①∴Sn-1=2an-1-2(n≥2,n∈N
*). ②①-②,得an=2an-2an-1(n≥2,n∈N
*).∵an≠0,∴=2(n≥2,n∈N
即数列{an}是等比数列.
∵a1=S1,
∴a1=2a1-2,即a1=2.
∴an=2n(n∈N
*).(2)证明
:∵对任意正整数n,总有bn=, ∴Tn=
=1+1＜2.
(3)解
:由(cn)n+1=an+1(n∈N*),知lncn=.令f(x)=
,则f′(x)=
.
∵在区间(0,e)上,f′(x)＞0,在区间(e,+∞)上,f′(x)＜0,
∴在区间(e,+∞)上f(x)为单调递减函数.
∴n≥2且n∈N
*时,{lncn}是递减数列.又lnc1＜lnc2,∴数列{lncn}中的最大项为lnc2=
ln3.
(文)解：
(1)∵xn+1-xn=(
)n,∴xn=x1+(x2-x1)+(x3-x2)+…+(xn-xn-1)
=1+(
)+(
)2+…+(
)n-1
=
=
.
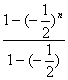
当n=1时上式也成立,
∴xn=
(n∈N
(2)an=
.
∵T2n=a1+2a2+3a3+…+(2n-1)a2n-1+2na2n
=(
)2+2(
)3+3(
)4+…+(2n-1)(
)2n+2n(
)2n+1, ①
∴
T2n=(
)3+2(
)4+3(
)5+…+(2n-1)(
)2n+1+2n(
)2n+2. ②
①-②,得
T2n=(
)2+(
)3+…+(
)2n+1-2n(
)2n+2.
∴
T2n=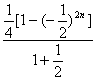
-2n(
)2n+2
=
.
∴T2n=
.
(3)由(2)可得9T2n=
.
又Qn=
,
当n=1时,22n=4,(2n+1)2=9,∴9T2n＜Qn;
当n=2时,22n=16,(2n+1)2=25,∴9T2n＜Qn;
当n≥3时,22n=［(1+1)n］2=(
)2＞(2n+1)2,
∴9T2n＞Qn.
综上所述,当n=1,2时,9T2n＜Qn;当n≥3时,9T2n＞Qn.