已知三个正数
满足
.
(1)若是从
中任取的三个数，求能构成三角形三边长的概率；
(2)若是从
中任取的三个数，求能构成三角形三边长的概率.
已知三个正数满足.
(1)若是从中任取的三个数，求能构成三角形三边长的概率；
(2)若是从中任取的三个数，求能构成三角形三边长的概率.
解:(1)若能构成三角形，则
.
①若
时，
.共1种； ②若
时。
.共2种；
同理
时，有3+1=4种； 
时，有4+2=6种；
时，有5+3+1=9种； 
时，有6+4+2=12种.
于是共有1+2+4+6+9+12=34种. -----------3分
从中任取的三个数()的种数
-----------5分
∴能构成三角形的概率为
.-------6分
(2)
能构成三角形的条件是
----8分
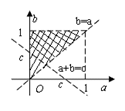
在坐标系
内画出满足以上条件的区域(如右图阴影部分)，由几何概型的计算方法可知，只求阴影部分的面积与图中正方形的面积比即可.又
，于是所要求的概率为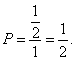
-----12分
又法：设