如图，在平面直角坐标系中，正方形
的顶点
与坐标原点重合，点
的坐标为（0,3），点
在
轴的正半轴上．直线
分别与边
相交于
两点，反比例函数
的图象经过点
并与边
相交于点
，连接
．点
是直线
上的动点，当
时，点的坐标是________________．
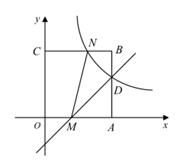
如图，在平面直角坐标系中，正方形的顶点与坐标原点重合，点的坐标为（0,3），点在轴的正半轴上．直线分别与边相交于两点，反比例函数的图象经过点并与边相交于点，连接．点是直线上的动点，当时，点的坐标是________________．
（1，0）或（3，2）
【解析】
根据正方形的性质以及一次函数表达式求出点D和点M坐标，从而求出反比例函数表达式，得到点N的坐标，求出MN，设点P坐标为（m，m-1），根据两点间距离表示出CP，得到方程，求解即可．
【详解】
解：∵正方形OABC的顶点O与坐标原点重合，点C的坐标为（0，3），
∴B（3，3），A（3，0），
∵直线y=x-1分别与边AB，OA相交于D，M两点，
∴可得：D（3，2），M（1，0），
∵反比例函数经过点D，
k=3×2=6，
∴反比例函数的表达式为
，令y=3，
解得：x=2，
∴点N的坐标为（2，3），
∴MN=
=
，
∵点P在直线DM上，
设点P的坐标为（m，m-1），
∴CP=
，
解得：m=1或3，
∴点P的坐标为（1，0）或（3，2）．
故答案为：（1，0）或（3，2）．
【点睛】
本题考查了正方形的性质，一次函数图象上点的坐标特征，两点之间的距离，反比例函数图象上点的坐标特征，解题的关键是根据点的坐标，利用待定系数法求出反比例函数解析式.