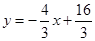 ,点A、D的坐标分别为(-4,0),(0,4). 动点P从A点出发,在AB边上匀速运动. 动点Q从点B出发,在折线BCD上匀速运动,速度均为每秒1个单位长度. 当其中一个动点到达终点时,另一动点也停止运动. 设点P运动t(秒)时,△OPQ的面积为S(不能构成△OPQ的动点除外).
,点A、D的坐标分别为(-4,0),(0,4). 动点P从A点出发,在AB边上匀速运动. 动点Q从点B出发,在折线BCD上匀速运动,速度均为每秒1个单位长度. 当其中一个动点到达终点时,另一动点也停止运动. 设点P运动t(秒)时,△OPQ的面积为S(不能构成△OPQ的动点除外).
【小题1】求出点C的坐标
【小题2】求S随t变化的函数关系式;
【小题3】当t为何值时,S有最大值?并求出这个最大值
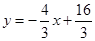 ,点A、D的坐标分别为(-4,0),(0,4). 动点P从A点出发,在AB边上匀速运动. 动点Q从点B出发,在折线BCD上匀速运动,速度均为每秒1个单位长度. 当其中一个动点到达终点时,另一动点也停止运动. 设点P运动t(秒)时,△OPQ的面积为S(不能构成△OPQ的动点除外).
,点A、D的坐标分别为(-4,0),(0,4). 动点P从A点出发,在AB边上匀速运动. 动点Q从点B出发,在折线BCD上匀速运动,速度均为每秒1个单位长度. 当其中一个动点到达终点时,另一动点也停止运动. 设点P运动t(秒)时,△OPQ的面积为S(不能构成△OPQ的动点除外).
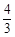 x+
x+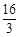 ,得x=1.
,得x=1.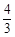 x+
x+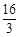 =0,
=0, =
= =5.
=5.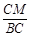 =
= .
.
 t.
t. OP·QN=
OP·QN= (4-t)×
(4-t)× t =-
t =-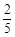 t2+
t2+ t(0<t<4). ……………2分
t(0<t<4). ……………2分
 t.
t. OP·QN=
OP·QN= ×(t-4)×
×(t-4)× t.
t.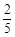 t2-
t2- t(4<t≤5). …………………………….3分
t(4<t≤5). …………………………….3分 ×OP×OD=
×OP×OD= (t-4)×4.
(t-4)×4.  .
.
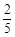 <0
<0 =2时,
=2时, =
= . ……………………………5分
. ……………………………5分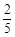 t2-
t2- t,对称轴为t=-
t,对称轴为t=-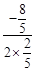 =2,
=2,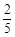 >0
>0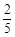 ×52-
×52- ×5=2. …………………………..6分
×5=2. …………………………..6分