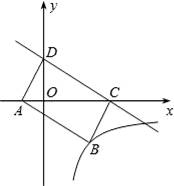
如图,直线y=﹣![]()
![]() x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y=
x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y=![]()
![]() 经过点B,与直线CD交于点E,则点E的坐标为( )
经过点B,与直线CD交于点E,则点E的坐标为( )

A.(![]()
![]() ,﹣
,﹣![]()
![]() ) B.(4,﹣
) B.(4,﹣![]()
![]() ) C.(
) C.(![]()
![]() ,﹣
,﹣![]()
![]() ) D.(6,﹣1)
) D.(6,﹣1)
如图,直线y=﹣![]()
![]() x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y=
x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y=![]()
![]() 经过点B,与直线CD交于点E,则点E的坐标为( )
经过点B,与直线CD交于点E,则点E的坐标为( )


A.(![]()
![]() ,﹣
,﹣![]()
![]() ) B.(4,﹣
) B.(4,﹣![]()
![]() ) C.(
) C.(![]()
![]() ,﹣
,﹣![]()
![]() ) D.(6,﹣1)
) D.(6,﹣1)
D【考点】反比例函数与一次函数的交点问题.
【分析】根据一次函数图象是点的坐标特征求得D(0,m),C(2m,0),然后根据垂线的性质求得A(﹣![]()
![]() m,0),进而根据三角形全等求得B(
m,0),进而根据三角形全等求得B(![]()
![]() m,﹣m),代入y=
m,﹣m),代入y=![]()
![]() 求得m的值,得出直线y=﹣
求得m的值,得出直线y=﹣![]()
![]() x+2,最后联立方程,解方程即可求得.
x+2,最后联立方程,解方程即可求得.
【解答】解:根据题意,直线y=﹣![]()
![]() x+m与x轴交于C,与y轴交于D,
x+m与x轴交于C,与y轴交于D,
分别令x=0,y=0,
得y=m,x=2m,
即D(0,m),C(2m,0),
又AD⊥DC且过点D,
所以直线AD所在函数解析式为:y=2x+m,
令y=0,得x=﹣![]()
![]() m,
m,
即A(﹣![]()
![]() m,0),
m,0),
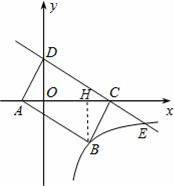
作BH⊥AC于H,
∵四边形ABCD是矩形,
∴AD=BC,∠DAO=∠BCH,
在△AOD和△CHB中
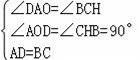

∴△AOD≌△CHB(AAS),
∴BH=OD=m,CH=OA=![]()
![]() m,
m,
∴OH=![]()
![]() m,
m,
∴B点的坐标为B(![]()
![]() m,﹣m)
m,﹣m)
又B在双曲线双曲线y=![]()
![]() (k<0)上,
(k<0)上,
∴![]()
![]() m•(﹣m)=﹣6,
m•(﹣m)=﹣6,
解得m=±2,
∵m>0,
∴m=2,
∴直线CD的解析式为y=﹣![]()
![]() x+2,
x+2,
解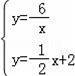
 ,
,
得![]()
![]() 和
和![]()
![]() ,
,
故点E的坐标为(6,﹣1),
故选D.

【点评】本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了三角形全等的判定与性质.