（1）求q的取值范围；
（2）设bn=an+2
an+1,记{bn}的前n项和为Tn，试比较Sn与Tn的大小.
（1）求q的取值范围；
（2）设bn=an+2an+1,记{bn}的前n项和为Tn，试比较Sn与Tn的大小.
当q=1时，Sn=na1＞0;
当q≠1时，Sn=＞0,即
＞0(n=1,2,3,…),上式等价于不等式组
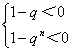(n=1,2,3,…) ①
或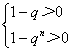
,(n=1,2,3,…). ②
解①式得q＞1，解②得-1＜q＜1.
综上，q的取值范围是（-1，0）∪(0,+∞).
（2）由bn=an+2
an+1得：bn=an(q2-
),
Tn=(q2-
)Sn,于是Tn-Sn=Sn(q+
)(q-2).
又因为Sn＞0，当-1＜q＜
时，Tn-Sn＞0，即Tn＞Sn;
当
＜q＜2且q≠0时，Tn-Sn＜0,即Tn＜Sn;
当q＞2时，Tn-Sn＞0,即Tn＞Sn.
当q=
或q=2时，Tn-Sn=0，即Tn=Sn.