已知曲线C 的极坐标方程是 ρ＝2，以极点为原点，极轴为 x 轴的正半轴建立平面直角坐标系, 直线 l 的参数方程为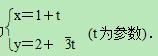
(Ⅰ)写出直线 l 的普通方程与曲线 C 的直角坐标方程；
(Ⅱ)设曲线C 经过伸缩变换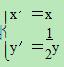
得到曲线 C′，设 M(x，y)为曲线 C′上任一点，
求 x2－ 3xy＋2y2 的最小值，并求相应点 M 的坐标
已知曲线C 的极坐标方程是 ρ＝2，以极点为原点，极轴为 x 轴的正半轴建立平面直角坐标系, 直线 l 的参数方程为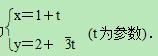
(Ⅰ)写出直线 l 的普通方程与曲线 C 的直角坐标方程；
(Ⅱ)设曲线C 经过伸缩变换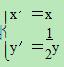得到曲线 C′，设 M(x，y)为曲线 C′上任一点，
求 x2－ 3xy＋2y2 的最小值，并求相应点 M 的坐标
解：(Ⅰ) 3x－y－ 3＋2＝0
x2＋y2＝4 4 分
 |
(Ⅱ)设 C′： 4 ＋y ＝1
设 M 为：x＝2cosθ，y＝sinθ 6 分
 |
x2－ 3xy＋2y2＝3＋2cos(2θ π 8 分 ＋ 3 )
所以当 M 为(1， 3 或(－1 3
，－
2 ) 2 )
x2－ 3xy＋2y2 的最小值为 1 10 分
－2x－2，x<－3，