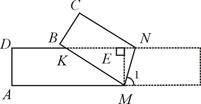
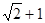 .在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.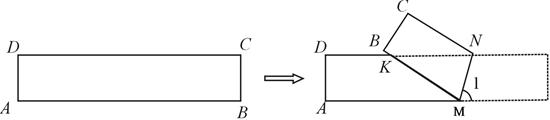
(1)若∠1=70°,求∠MKN的度数.
(2)△MNK的面积能否小于
 ?若能,求出此时∠1的度数;若不能,试说明理由.
?若能,求出此时∠1的度数;若不能,试说明理由.(3)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值及∠1的度数。
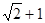 .在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
 ?若能,求出此时∠1的度数;若不能,试说明理由.
?若能,求出此时∠1的度数;若不能,试说明理由.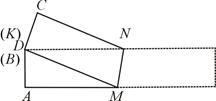
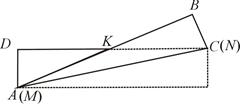
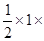 KN=
KN=
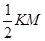 ,所以KM最小值为1,即KM⊥AM,所以∠MNK=∠1=45°,此时△MNK的面积最小为
,所以KM最小值为1,即KM⊥AM,所以∠MNK=∠1=45°,此时△MNK的面积最小为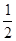 ,所以此三角形面积不能小于
,所以此三角形面积不能小于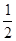 (5分)
(5分)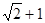 - x,由勾股定理,得
- x,由勾股定理,得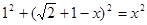 ,
,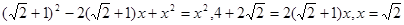 ,所以
,所以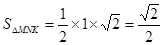 Sin∠AMD=
Sin∠AMD=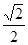
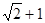 -x,同理可得
-x,同理可得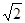
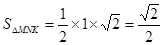
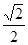 , ∠AKD=45°, ∠1=22.5°
, ∠AKD=45°, ∠1=22.5°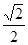 ,∠1=67.5°或22.5° (10分)解析:
,∠1=67.5°或22.5° (10分)解析: