如图,已知A(1,1),B(5,4),C(2,5),设向量![]() 是与向量
是与向量![]() 垂直的单位向量.
垂直的单位向量.
(1)求单位向量![]() 的坐标;
的坐标;
(2)求向量![]() 在向量
在向量![]() 上的投影;
上的投影;
(3)求△ABC![]() 的面积S△ABC.
的面积S△ABC.
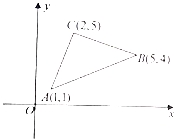
如图,已知A(1,1),B(5,4),C(2,5),设向量![]() 是与向量
是与向量![]() 垂直的单位向量.
垂直的单位向量.
(1)求单位向量![]() 的坐标;
的坐标;
(2)求向量![]() 在向量
在向量![]() 上的投影;
上的投影;
(3)求△ABC![]() 的面积S△ABC.
的面积S△ABC.

【考点】平面向量数量积的运算;平面向量的坐标运算.
【专题】计算题;转化思想;分析法;平面向量及应用.
【分析】(1)设![]() =(x,y),根据向量的数量积和向量的模得到
=(x,y),根据向量的数量积和向量的模得到![]() ,解方程得,
,解方程得,
(2)设向量![]() 与向量
与向量![]() 的夹角为θ,在
的夹角为θ,在![]() 上的投影为h,根据向量的投影即可求出.
上的投影为h,根据向量的投影即可求出.
(3)根据三角形的面积公式即可求出.
【解答】解:(1)设![]() =(x,y),依题意有,
=(x,y),依题意有,
![]() =(4,3),|
=(4,3),|![]() |=5,|
|=5,|![]() |=1,
|=1,![]() ⊥
⊥![]() ,即
,即![]() =0,
=0,
有![]() ,解得
,解得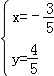 ,或
,或![]()
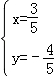 ,
,
所以,![]() =(﹣
=(﹣![]() ,
,![]() )或
)或![]() =(
=(![]() ,﹣
,﹣![]() ),
),
(2)设向量![]() 与向量
与向量![]() 的夹角为θ,在
的夹角为θ,在![]() 上的投影为h,
上的投影为h,
则h=|![]() |cosθ=
|cosθ=![]() =
=![]() •
•![]() ,
,![]() =(1,4),
=(1,4),
当![]() =(﹣
=(﹣![]() ,
,![]() )时,h=1×(﹣
)时,h=1×(﹣![]() )+4×
)+4×![]() =
=![]() ,
,
当![]() =(
=(![]() ,﹣
,﹣![]() )时,h=1×
)时,h=1×![]() +4×(﹣
+4×(﹣![]() )=﹣
)=﹣![]() ,
,
(3)S△ABC=![]() |
|![]() ||h|=
||h|=![]() ×5×
×5×![]() =
=![]() .
.
【点评】本题考查了向量的数量![]() 积运算和向量的模的计算,以及向量的投影和三角形的面积.
积运算和向量的模的计算,以及向量的投影和三角形的面积.