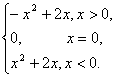
(1)求实数m的值，并在给出图的直角坐标系中画出y=f(x)的图像；
(2)若函数f(x)在区间［-1，|a|-2］上单调递增，试确定a的取值范围.
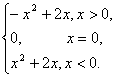
(1)求实数m的值，并在给出图的直角坐标系中画出y=f(x)的图像；
(2)若函数f(x)在区间［-1，|a|-2］上单调递增，试确定a的取值范围.
解：
(1)当x＜0时，-x＞0，f(-x)=-(-x)2+2(-x)=-x2-2x.又f(x)为奇函数，∴f(-x)=-f(x)=-x2-2x.∴f(x)=x2＋2x.
∴m=2.
函数y=f(x)的图像如下图所示.
(2)由(1),知f(x)=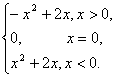
由图像可知，f(x)在［-1，1］上单调递增，要使f(x)在［-1，|a|-2］上单调递增，
则有［-1，|a|-2］
［-1，1］，所以有
解之,得-3≤a＜-1,或1＜a≤3.